Naive Model

Naive model

A simple OLS model with temperature and air humidity, without any transformation or feature engineering -no thinking at all-.

⏩ stepit 'naive': Starting execution of `strom.modelling.assess_model()` 2025-11-24 03:24:46

⏩ stepit 'get_single_split_metrics': Starting execution of `strom.modelling.get_single_split_metrics()` 2025-11-24 03:24:46

✅ stepit 'get_single_split_metrics': Successfully completed and cached [exec time 0.0 seconds, cache time 0.0 seconds, size 1.0 KB] `strom.modelling.get_single_split_metrics()` 2025-11-24 03:24:46

♻️  stepit 'cross_validate_pipe': is up-to-date. Using cached result for `strom.modelling.cross_validate_pipe()` 2025-11-24 03:24:46

✅ stepit 'naive': Successfully completed and cached [exec time 0.1 seconds, cache time 0.0 seconds, size 14.6 KB] `strom.modelling.assess_model()` 2025-11-24 03:24:46

Metrics

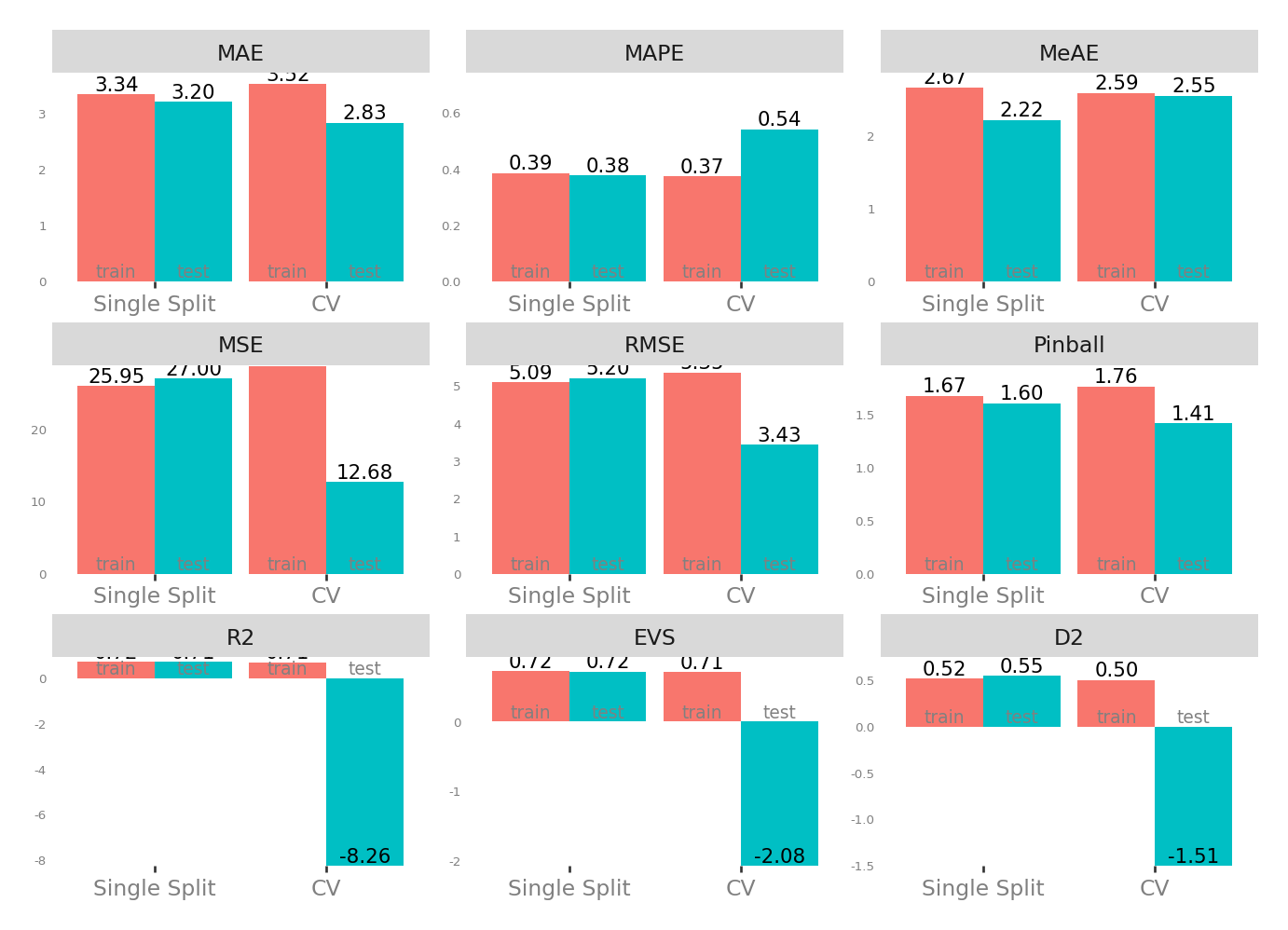
	Single Split		CV
	train	test	test	train
MAE - Mean Absolute Error	3.340724	3.204808	2.826912	3.521417
MSE - Mean Squared Error	25.954378	27.002107	12.680772	28.653635
RMSE - Root Mean Squared Error	5.094544	5.196355	3.427023	5.350081
R2 - Coefficient of Determination	0.721536	0.714094	-8.261011	0.710489
MAPE - Mean Absolute Percentage Error	0.385572	0.377010	0.542071	0.374245
EVS - Explained Variance Score	0.721536	0.715016	-2.078617	0.710489
MeAE - Median Absolute Error	2.667585	2.218728	2.553731	2.590863
D2 - D2 Absolute Error Score	0.517719	0.549459	-1.508520	0.504136
Pinball - Mean Pinball Loss	1.670362	1.602404	1.413456	1.760708

Scatter plot matrix

Observed vs. Predicted and Residuals vs. Predicted

Check for …

check the residuals to assess the goodness of fit.

white noise or is there a pattern?
heteroscedasticity?
non-linearity?

Normality of Residuals:

Check for …

Are residuals normally distributed?

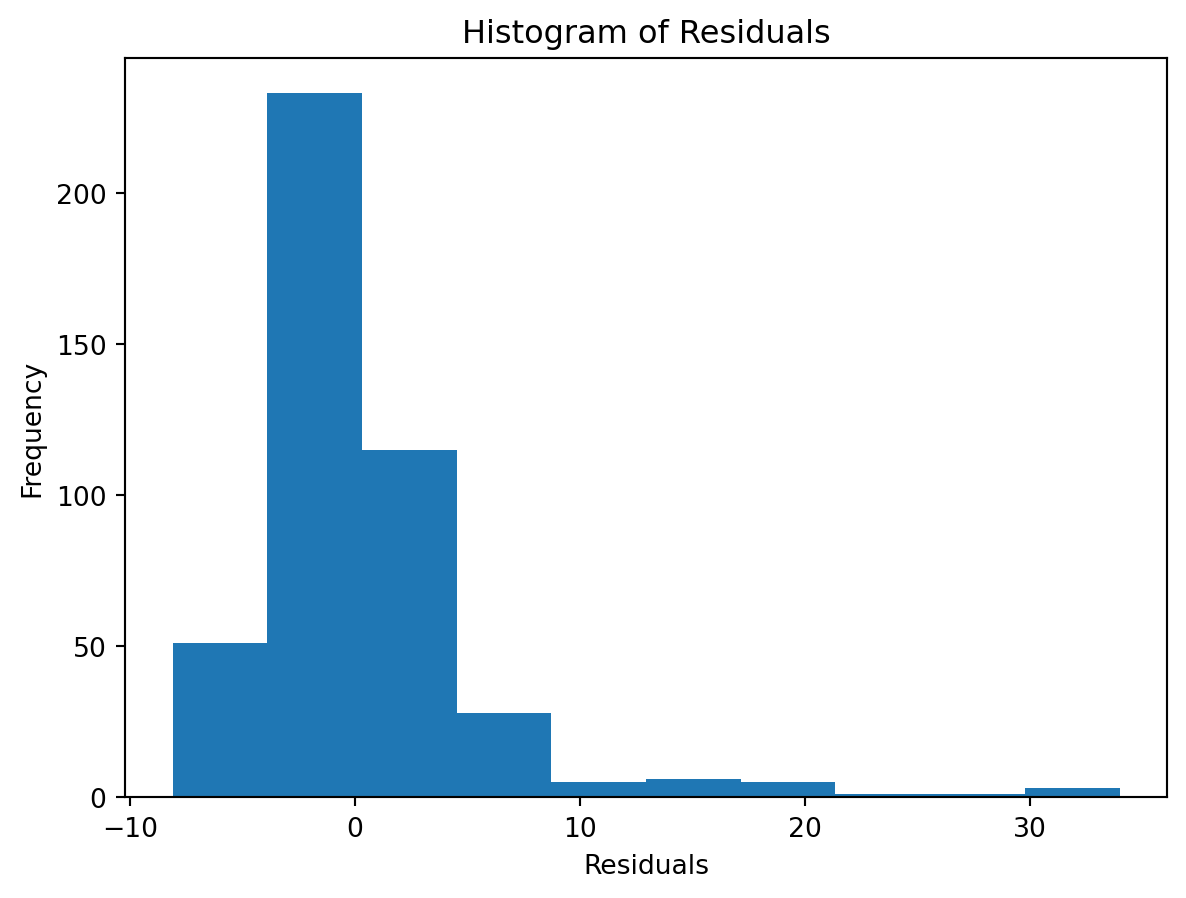
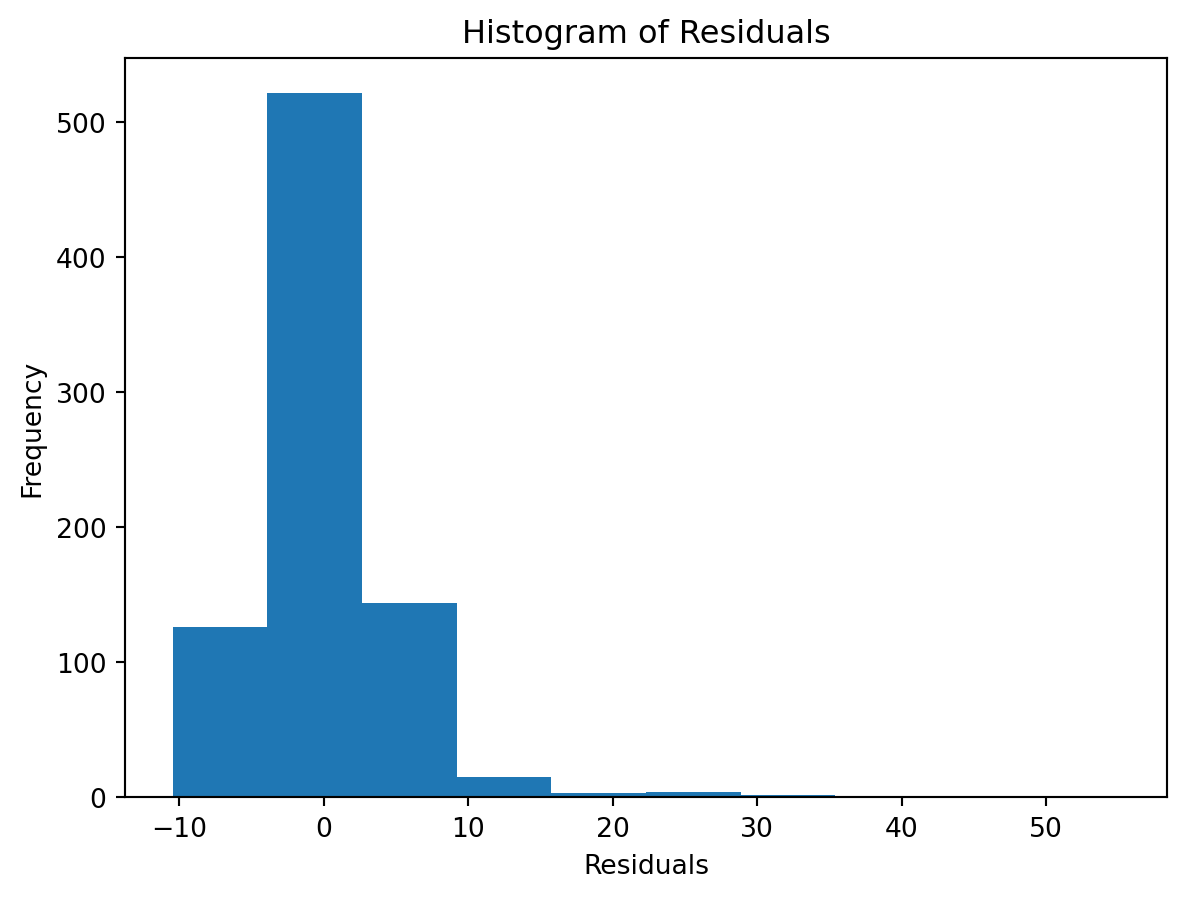
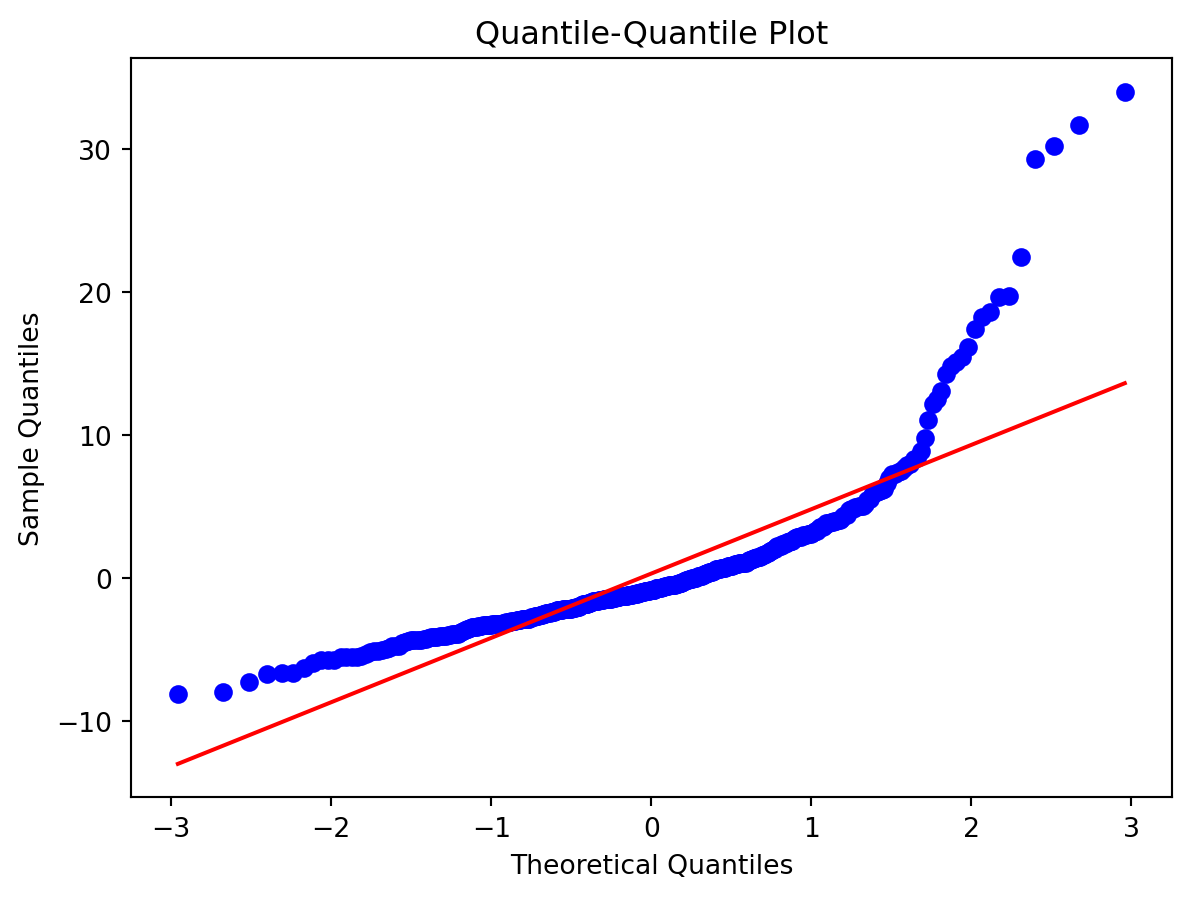
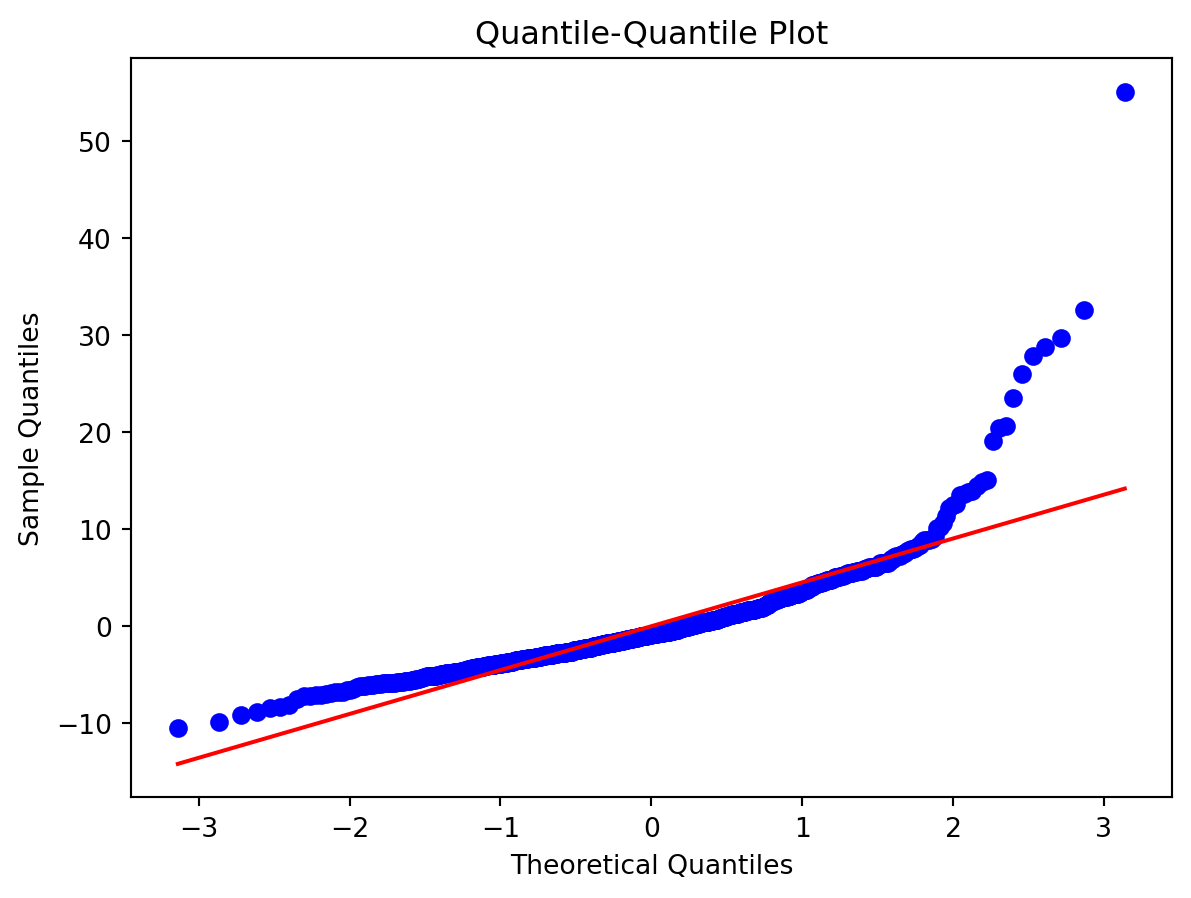
Leverage

Scale-Location plot

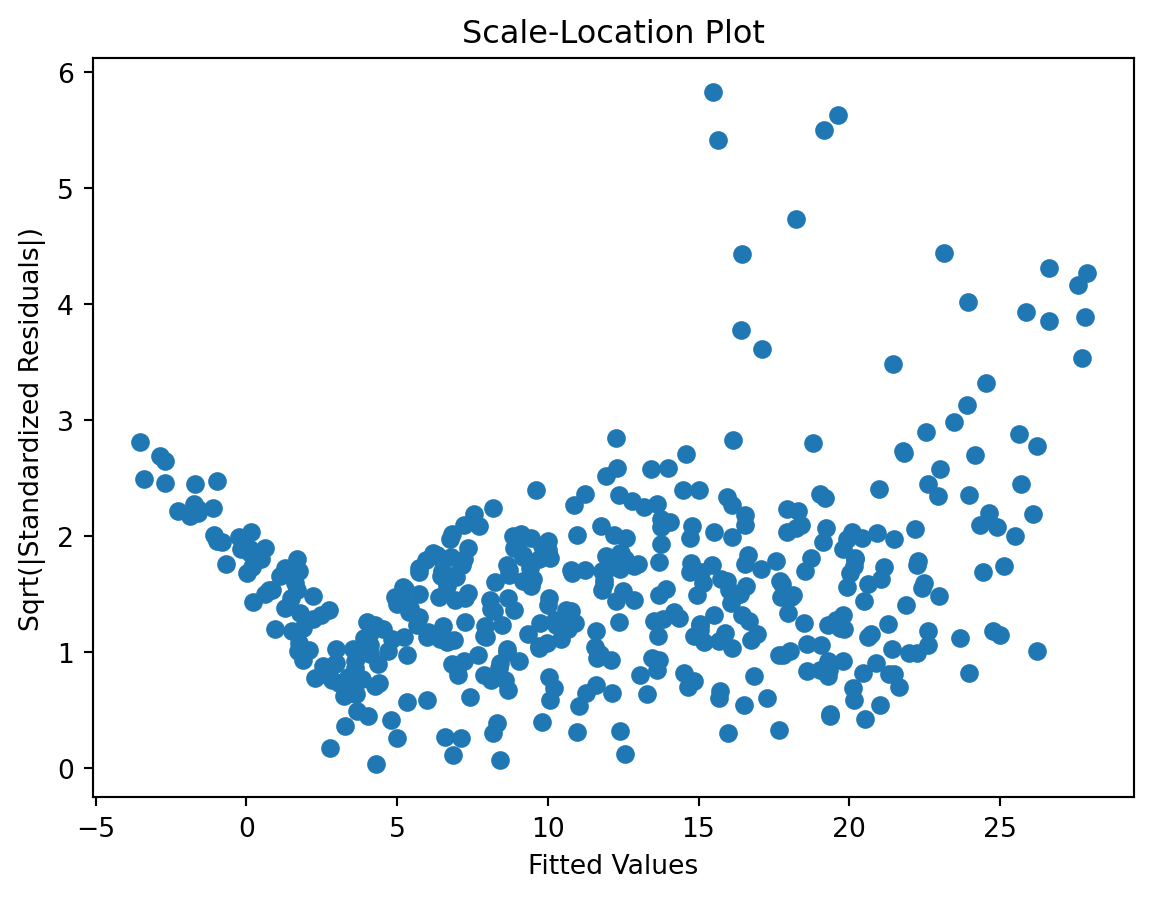
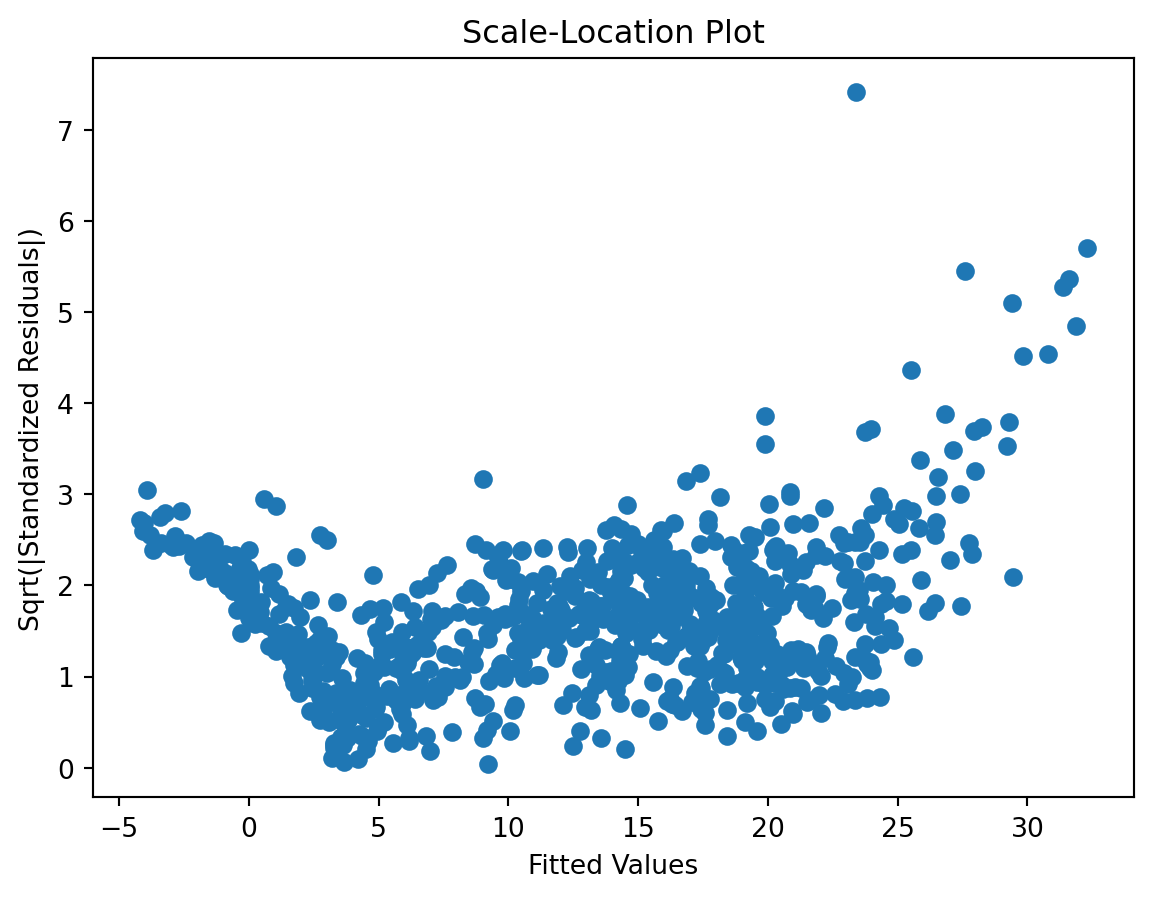
Residuals Autocorrelation Plot

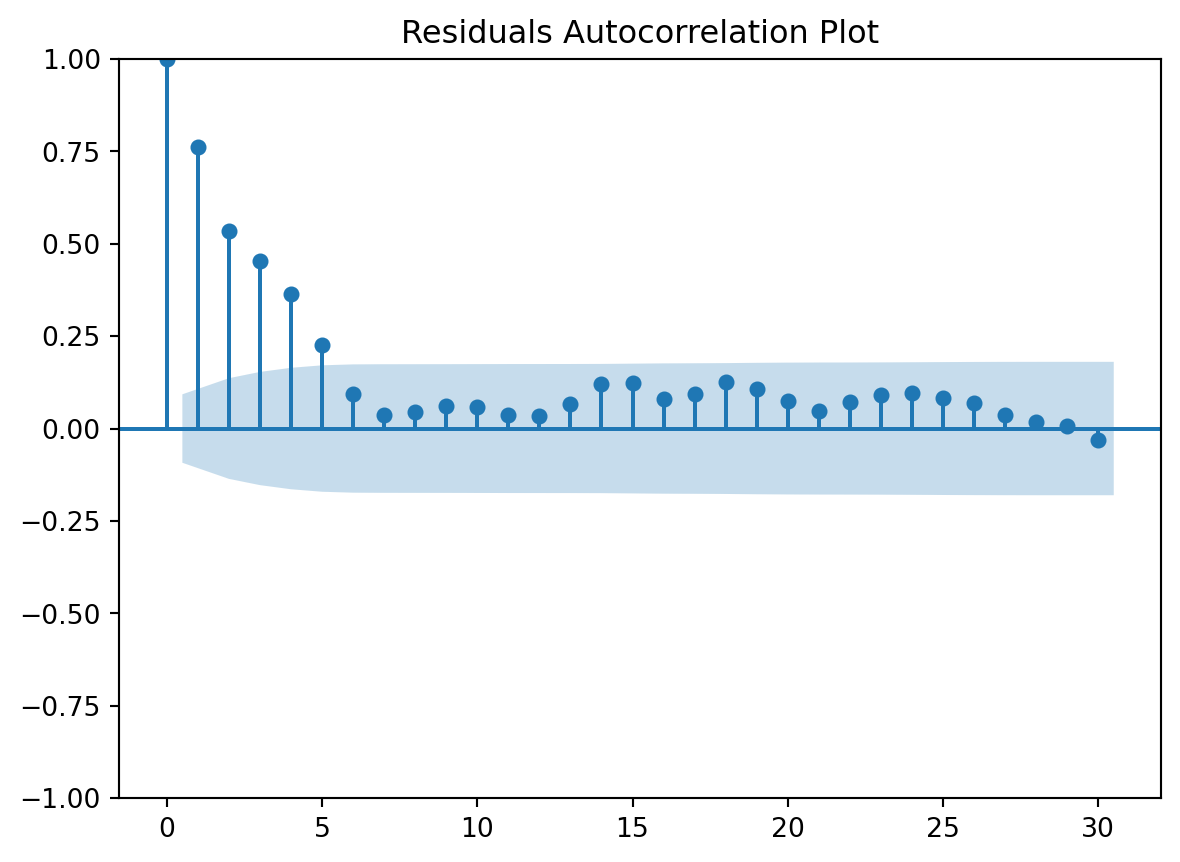
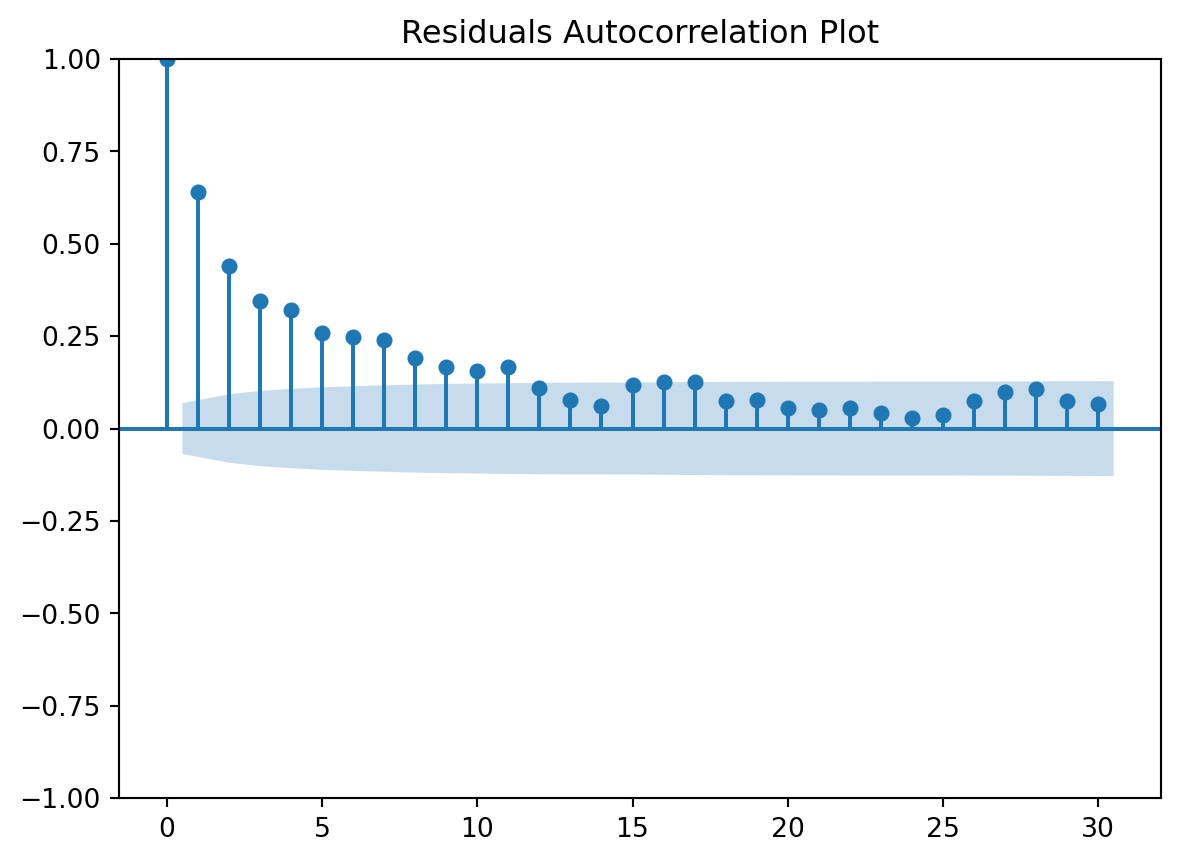
Residuals vs Time

TODOs

Clearly the naive model is not a good fit (as expected).

Listing 1

It needs a polynomial with the temperature (second order perhaps)
Check if the association with relative humidity, if it is just an artifact of the correlation with temperature, or if there might something meaningful going on there
and bring other climatic data, rainfall and snowfall might be relevant

Naive Model, but using statsmodels …

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                     wd   R-squared:                       0.720
Model:                            OLS   Adj. R-squared:                  0.720
Method:                 Least Squares   F-statistic:                     1623.
Date:                Mon, 24 Nov 2025   Prob (F-statistic):               0.00
Time:                        03:24:50   Log-Likelihood:                -3857.8
No. Observations:                1264   AIC:                             7722.
Df Residuals:                    1261   BIC:                             7737.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         27.2464      1.296     21.031      0.000      24.705      29.788
tt_tu_mean    -1.1233      0.021    -54.357      0.000      -1.164      -1.083
rf_tu_mean    -0.0532      0.015     -3.502      0.000      -0.083      -0.023
==============================================================================
Omnibus:                      900.412   Durbin-Watson:                   0.625
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            19753.299
Skew:                           3.032   Prob(JB):                         0.00
Kurtosis:                      21.393   Cond. No.                         724.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R-squared: 0.720218658535322

Naive model, but using scikit-learn without pipeline …